本文的目的总结一些标量衍射的计算方法,并讨论讨论他们的适用条件。代码和例子在:https://github.com/sleepingcat42/Scalardiffraction
需要的预备知识:涉及的数理知识并不高深,主要是线性系统和傅里叶变换(离散傅里叶变换)的基础知识,当然还有光学。
涉及的内容:准确地说,应该是讨论基于快速傅里叶变换(FFT)的标量衍射,主要是常见的几种衍射计算方法
瑞利-索末菲/角谱衍射
菲涅尔衍射(Fres-TF 和 Fres-IR)
其他衍射计算方法(待补充)
单步菲涅尔衍射
两步菲涅尔衍射
夫琅禾费衍射
其他(未来补充)
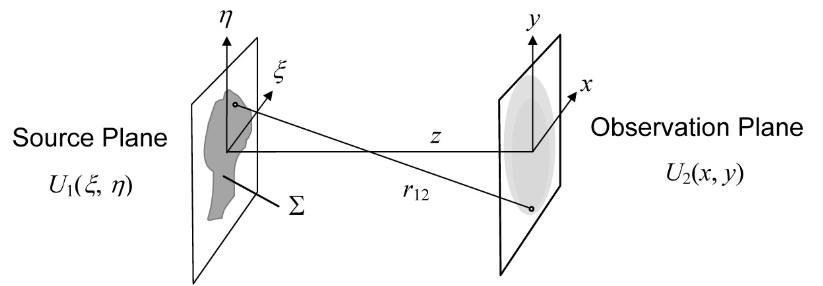
本文的重点并不在标量衍射的推导,所以跳过麦克斯韦方程组,和参考文献[2 ] 类似,直接到跳到第一类瑞利-索末菲积分
U 2 ( x , y ) = 1 j λ ∬ Σ U 1 ( ξ , η ) z r 12 exp ( j k r 12 ) r 12 d ξ d η U_2(x, y)=\frac{1}{j \lambda} \iint_{\Sigma} U_1(\xi, \eta) \frac{z}{r_{12}} \frac{\exp \left(j k r_{12}\right)}{r_{12}} d \xi d \eta
U 2 ( x , y ) = j λ 1 ∬ Σ U 1 ( ξ , η ) r 1 2 z r 1 2 exp ( j k r 1 2 ) d ξ d η
λ \lambda λ k = 2 π k=2\pi k = 2 π ( x , y ) (x, y) ( x , y ) ( ξ , η ) (\xi, \eta) ( ξ , η ) U 1 U_1 U 1 U 2 U_2 U 2 Σ \Sigma Σ z z z 2+(x-\xi) 2+(y-\eta)^2} $ 。
当然,我们可以直接计算这个积分。假设采样数为 N × N N\times N N × N
积分公式可以改写成卷积的形式
U 2 ( x , y ) = ∬ U 1 ( ξ , η ) h ( x − ξ , y − η ) d ξ d η , U_2(x, y)=\iint U_1(\xi, \eta) h(x-\xi, y-\eta) d \xi d \eta,
U 2 ( x , y ) = ∬ U 1 ( ξ , η ) h ( x − ξ , y − η ) d ξ d η ,
其中
h ( x , y ) = z j λ exp ( j k r ) r 2 h(x, y)=\frac{z}{j \lambda} \frac{\exp (j k r)}{r^2}
h ( x , y ) = j λ z r 2 exp ( j k r )
为 R-S 积分的冲激响应(impulse response)
可以证明 R-S 积分传递函数(transfer function)的函数为
H ( f X , f Y ) = exp ( j k z 1 − ( λ f X ) 2 − ( λ f Y ) 2 ) H\left(f_X, f_Y\right)=\exp \left(j k z \sqrt{1-\left(\lambda f_X\right)^2-\left(\lambda f_Y\right)^2}\right)
H ( f X , f Y ) = exp ( j k z 1 − ( λ f X ) 2 − ( λ f Y ) 2 )
f X f_X f X f Y f_Y f Y X X X Y Y Y h ( x , y ) h(x, y) h ( x , y ) H ( f X , f Y ) H(f_X, f_Y) H ( f X , f Y ) 3 ]。
这样,就有两种方法去计算:第一种是基于冲击响应的卷积方法
U 2 ( x , y ) = F − 1 { I { U 1 ( x , y ) } F { h ( x , y ) } } U_2(x, y)=\mathfrak{F}^{-1}\left\{\mathfrak{I}\left\{U_1(x, y)\right\} \mathfrak{F}\{h(x, y)\}\right\}
U 2 ( x , y ) = F − 1 { I { U 1 ( x , y ) } F { h ( x , y ) } }
另一种是基于传递函数的方法
U 2 ( x , y ) = F − 1 { F { U 1 ( x , y ) } H ( f X , f Y ) } U_2(x, y)=\mathfrak{F}^{-1}\left\{\mathfrak{F}\left\{U_1(x, y)\right\} H\left(f_X, f_Y\right)\right\}
U 2 ( x , y ) = F − 1 { F { U 1 ( x , y ) } H ( f X , f Y ) }
F \mathfrak{F} F F − 1 \mathfrak{F}^{-1} F − 1
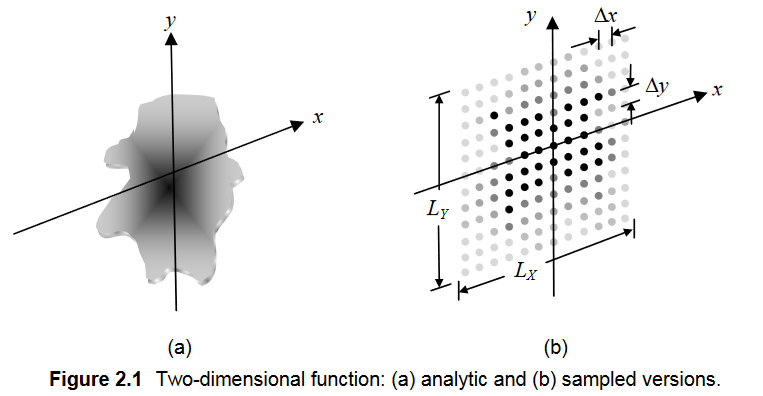
假设对光场的离散采样如下图所示,X X X Y Y Y L X L_X L X L Y L_Y L Y [ − 1 2 L X , 1 2 L X ] \left[ -\frac{1}{2}L_X, \frac{1}{2}L_X\right] [ − 2 1 L X , 2 1 L X ] [ − 1 2 L Y , 1 2 L Y ] \left[ -\frac{1}{2}L_Y, \frac{1}{2}L_Y\right] [ − 2 1 L Y , 2 1 L Y ] Δ x \Delta x Δ x Δ y \Delta y Δ y N y = L y Δ y N_y = \frac{L_y}{\Delta y} N y = Δ y L y
为了简化讨论,考虑一维的情形,对于
h ( x ) = z j λ exp ( j k r ) r 2 = z j λ exp ( j ϕ h ( x ) ) r 2 h(x)=\frac{z}{j \lambda} \frac{\exp (j k r)}{r^2} = \frac{z}{j \lambda} \frac{\exp (j \phi_h(x))}{r^2}
h ( x ) = j λ z r 2 exp ( j k r ) = j λ z r 2 exp ( j ϕ h ( x ) )
其中
ϕ h = k z 2 + x 2 \phi_h = k \sqrt{z^2+x^2}
ϕ h = k z 2 + x 2
其局域空间频率应小于奈奎斯特采样频率
∣ 1 2 π ∂ ϕ h ∂ x ∣ m a x ≤ 1 2 Δ x \left| \frac{1}{2 \pi} \frac{\partial \phi_h}{\partial x} \right|_{max} \leq \frac{1}{2 \Delta x}
∣ ∣ ∣ ∣ ∣ 2 π 1 ∂ x ∂ ϕ h ∣ ∣ ∣ ∣ ∣ m a x ≤ 2 Δ x 1
即
∣ x λ z 2 + x 2 ∣ m a x ≤ 1 2 Δ x \left| \frac{x}{\lambda\sqrt{z^2 + x^2}}\right|_{max} \leq \frac{1}{2 \Delta x}
∣ ∣ ∣ ∣ ∣ λ z 2 + x 2 x ∣ ∣ ∣ ∣ ∣ m a x ≤ 2 Δ x 1
整理得到
z ≥ 2 x m a x Δ x λ 1 − ( λ 2 Δ x ) 2 z \geq \frac{ 2x_{max}\Delta x}{\lambda} \sqrt{1- \left(\frac{\lambda}{2\Delta x}\right)^2}
z ≥ λ 2 x m a x Δ x 1 − ( 2 Δ x λ ) 2
x x x x m a x = L 2 x_{max} = \frac{L}{2} x m a x = 2 L L X = N x Δ x L_X = N_x \Delta x L X = N x Δ x
z ≥ L X Δ x λ 1 − ( λ 2 Δ x ) 2 = N x Δ x 2 λ 1 − ( λ 2 Δ x ) 2 z \geq \frac{ L_X \Delta x}{\lambda} \sqrt{1- \left(\frac{\lambda}{2\Delta x}\right)^2} = \frac{ N_x \Delta x^2}{\lambda} \sqrt{1- \left(\frac{\lambda}{2\Delta x}\right)^2}
z ≥ λ L X Δ x 1 − ( 2 Δ x λ ) 2 = λ N x Δ x 2 1 − ( 2 Δ x λ ) 2
上式并不适合衍射距离确定的采样讨论,当距离一定,整理上式得到采样间隔 Δ x \Delta x Δ x
Δ x ≤ λ z L 1 + ( L 2 z ) 2 \Delta x \leq \frac{\lambda z}{ L} \sqrt{1+ \left( \frac{L}{2z}\right)^2}
Δ x ≤ L λ z 1 + ( 2 z L ) 2
H ( f X ) = exp ( j k z 1 − ( λ f X ) 2 ) = exp ( j ϕ H ( f X ) ) H\left(f_X\right)=\exp \left(j k z \sqrt{1-\left(\lambda f_X\right)^2}\right) = \exp \left(j \phi_H(f_X)\right)
H ( f X ) = exp ( j k z 1 − ( λ f X ) 2 ) = exp ( j ϕ H ( f X ) )
其中 $ \phi_H(f_X) = k z \sqrt{1-\left(\lambda f_X\right)^2}$ 应该满足以下采样条件
∣ 1 2 π ∂ ϕ H ( f X ) ∂ f X ∣ max ≤ 1 2 Δ f X , \left|\frac{1}{2 \pi} \frac{\partial \phi_H\left(f_X\right)}{\partial f_X}\right|_{\max } \leq \frac{1}{2 \Delta f_X},
∣ ∣ ∣ ∣ ∣ 2 π 1 ∂ f X ∂ ϕ H ( f X ) ∣ ∣ ∣ ∣ ∣ m a x ≤ 2 Δ f X 1 ,
得到
∣ z λ f X 1 − ( λ f X ) 2 ∣ max ≤ 1 2 Δ f X , \left|\frac{z \lambda f_X}{\sqrt{1 - \left( \lambda f_X\right)^2}} \right|_{\max } \leq \frac{1}{2 \Delta f_X},
∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 − ( λ f X ) 2 z λ f X ∣ ∣ ∣ ∣ ∣ ∣ ∣ m a x ≤ 2 Δ f X 1 ,
式子左边是增函数,当 f X f_X f X f X m a x = 1 2 Δ x {f_X}_{max} = \frac{1}{2 \Delta x} f X m a x = 2 Δ x 1 Δ f X = 1 L \Delta f_X = \frac{1}{L} Δ f X = L 1
z ≤ 2 x m a x Δ x λ 1 − ( λ 2 Δ x ) 2 z \leq \frac{ 2x_{max}\Delta x}{\lambda} \sqrt{1- \left(\frac{\lambda}{2\Delta x}\right)^2}
z ≤ λ 2 x m a x Δ x 1 − ( 2 Δ x λ ) 2
刚好与冲激响应函数相反,同样在衍射距离 z z z Δ x \Delta x Δ x
Δ x ≥ λ z L 1 + ( L 2 z ) 2 \Delta x \geq \frac{\lambda z}{ L} \sqrt{1+ \left( \frac{L}{2z}\right)^2}
Δ x ≥ L λ z 1 + ( 2 z L ) 2
再次回到 R-S 积分
U 2 ( x , y ) = 1 j λ ∬ Σ U 1 ( ξ , η ) z r 12 exp ( j k r 12 ) r 12 d ξ d η U_2(x, y)=\frac{1}{j \lambda} \iint_{\Sigma} U_1(\xi, \eta) \frac{z}{r_{12}} \frac{\exp \left(j k r_{12}\right)}{r_{12}} d \xi d \eta
U 2 ( x , y ) = j λ 1 ∬ Σ U 1 ( ξ , η ) r 1 2 z r 1 2 exp ( j k r 1 2 ) d ξ d η
在旁轴近似条件, 衍射角很小, z ≫ L z \gg L z ≫ L r 12 r_{12} r 1 2
r 12 = z 2 + ( x − ξ ) 2 + ( y − η ) 2 ≈ z [ 1 + 1 2 ( x − ξ z ) 2 + 1 2 ( y − η z ) 2 ] r_{12}=\sqrt{z^2+(x-\xi)^2+(y-\eta)^2} \approx z\left[1+\frac{1}{2}\left(\frac{x-\xi}{z}\right)^2+\frac{1}{2}\left(\frac{y-\eta}{z}\right)^2\right]
r 1 2 = z 2 + ( x − ξ ) 2 + ( y − η ) 2 ≈ z [ 1 + 2 1 ( z x − ξ ) 2 + 2 1 ( z y − η ) 2 ]
最后得到菲涅尔衍射的冲激响应
h ( x , y ) = 1 j λ z exp ( j k z ) exp ( [ j k 2 z ( x 2 + y 2 ) ] h(x, y) = \frac{1}{j\lambda z}\exp(jkz) \exp(\left[\frac{jk}{2z}\left(x^2+y^2\right)\right]
h ( x , y ) = j λ z 1 exp ( j k z ) exp ( [ 2 z j k ( x 2 + y 2 ) ]
传递函数,也就是上式的里叶变换
H ( f X , f Y ) = exp ( j k z ) exp [ − j π λ z ( f X 2 + f Y 2 ) ] H(f_{X},f_{Y}) =\exp(j k z)\exp\left[ -j\pi\lambda z\left( {f_X}^2 + {f_Y}^2\right)\right]
H ( f X , f Y ) = exp ( j k z ) exp [ − j π λ z ( f X 2 + f Y 2 ) ]
其采样条件可以利用上一节得到的结果在傍轴近似下得到,对于冲激响应 h,当 z ≫ L z \gg L z ≫ L
Δ x ≤ λ z L 1 + ( L 2 z ) 2 ≈ λ z L \Delta x \leq \frac{\lambda z}{ L} \sqrt{1+ \left( \frac{L}{2z}\right)^2} \approx \frac{\lambda z}{ L}
Δ x ≤ L λ z 1 + ( 2 z L ) 2 ≈ L λ z
传播距离 z z z
z ≥ L X Δ x λ z \geq \frac{ L_X \Delta x}{\lambda}
z ≥ λ L X Δ x
对于传递函数 H
Δ x ≥ λ z L \Delta x \geq \frac{\lambda z}{L}
Δ x ≥ L λ z
z ≤ L X Δ x λ z \leq \frac{ L_X \Delta x}{\lambda}
z ≤ λ L X Δ x
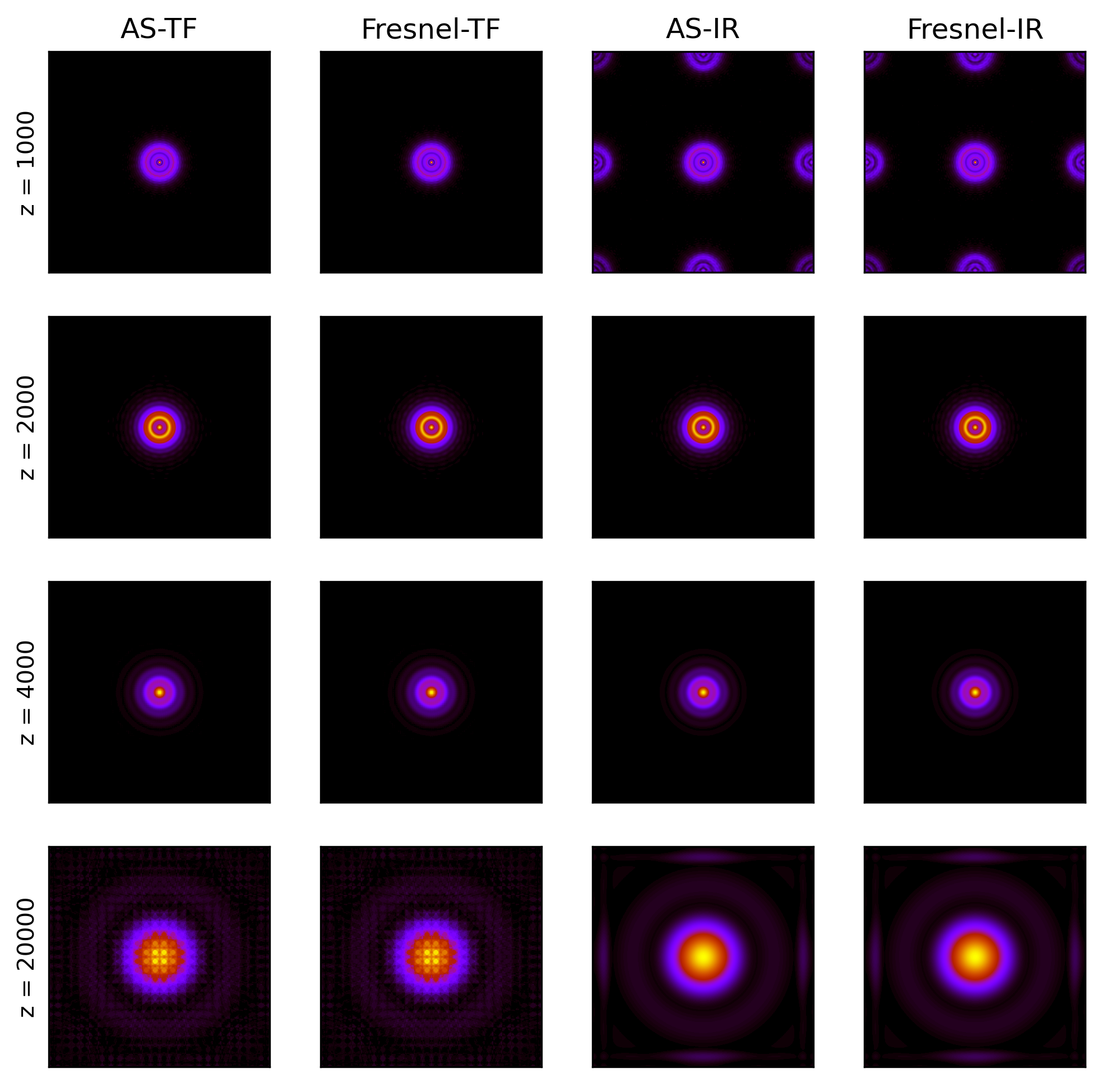
仿真参数设置下图代码段所示,可以计算出在 z = 2000 z=2000 z = 2 0 0 0 z > 2000 z >2000 z > 2 0 0 0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 import numpy as np from scalardifflib import propagation_tf, propagation_irfrom mathfunc import circfrom matplotlib import pyplot as plt0.5 256 0.5e-6 0.05 2 , L/2 -L/Nx, Nx)2 +y**2 )/r**2 )'AS' , 'Fresnel' ] 'TF' , 'IR' ]1000 ,2000 ,4000 ,20000 ]print (' zc = ' ,str (L*dx/wavelen), 'mm' )lambda kernel, method, z: propagation_tf(u1, L, wavelen,z,kernel) if method =='TF' else propagation_ir(u1, L, wavelen,z,kernel) 8 , 8 ), dpi=300 )1 for i in range (len (z)):for j in range (len (kernels)):for k in range (len (methods)):4 ,4 ,figindx)abs (u2)**2 , 'gnuplot' )if (figindx-1 ) % 4 ==0 :'z = ' +str (z[i]))if figindx <= 4 :'-' +methods[j])1
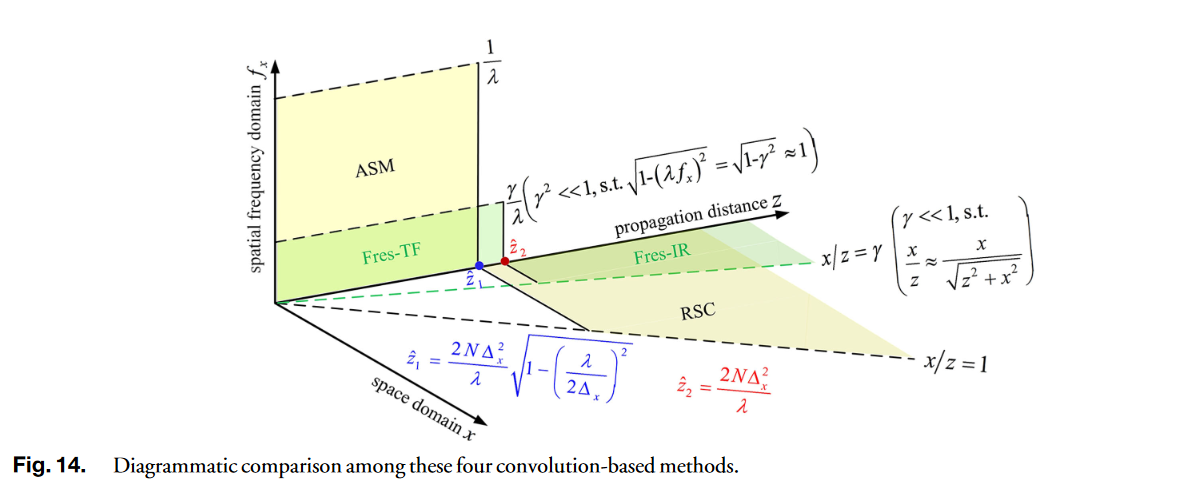
借用文献的一张图,这四种衍射计算方法的使用范围
Goodman, Joseph W. Introduction to Fourier optics. Roberts and Company publishers, 2005.
Voelz, David George. Computational fourier optics: a MATLAB tutorial. Vol. 534. Bellingham, Washington: SPIE press, 2011.
Ersoy, Okan K. Diffraction, Fourier optics and imaging. John Wiley & Sons, 2006..
Zhang, Wenhui, et al. "Analysis of numerical diffraction calculation methods: from the perspective of phase space optics and the sampling theorem." JOSA A 37.11 (2020): 1748-1766.